Transforming Task Representations To Allow Deep Learning Models to Perform Novel Tasks

A Brief Summary of a Long Paper

Written and presented for the 25th meeting of the SF FastAI Study Group.

In this review we'll look at a recent research paper: "Transforming task representations to allow deep learning models to perform novel tasks" by Andrew K. Lampinen and James L. McClelland of Stanford.

This paper caught my eye because it's not domain specific. The authors apply a general technique to achieve excellent performance across domains. The authors' proposed "meta-mapping" approach fits a higher level pattern also on display with transfer learning, pre-training, and "conditioning" a recurrent neural network.

At the time of writing this paper has not been widely noticed: the HoMM (homoicon meta mapping) repository has one star on Github (mine).

This review focuses on understanding the model's architecture, the concept of 'meta-mapping', and it's relevance for Deep Learning practitioners.

The Problem: Models Don't Adapt

Deep Learning models are fragile. Even models with superhuman performance on specific tasks fail when the task is even slightly altered. Human brains, by contrast, are much more adaptable.

If told to "lose at poker" a human can easily invert their skill at winning poker and apply it to the altered task. If told to identify a shape in a new color or texture, a human can do so — even if they've never seen the shape in that color or texture before.

The challenge of adapting to a problem not seen during training is called "zero shot" learning. This paper reframes the problem of "zero shot" learning by asking a model to learn representations of tasks.

These representations are encoded as examples or written instructions. This "task representation" is then used, similar to pre-training, to adapt a model to adjacent tasks and to speed up training.

The Outcome: Good Zero-Shot Learning

The author's find solid performance across domains. In a card game experiment, image classification, reinforcement learning, and regression, the authors' meta-mapping approach achieves 80-90% performance, with no data, on a novel task that contradicts the model's prior experience.

Meta-mapping (and here I'm editorializing a bit) seems to have transfer learning-like outcomes. The authors use meta-mapping as a starting point for training new models and find that it can substantially reduce learning time and cumulative error.

The Model: Task to Action

The model begins from the standard deep learning assumption that a "task" is a mapping of inputs to outputs (ex. images —> labels).

The architecture has two main pieces: a network concerned with "understanding" the task -- which here I'll call the "mapping network" -- and a network that does the task itself -- which the authors refer to the the "action network".

The paper introduces the concept of a homoiconic meta-mapping (HoMM): a mapping between a task representation (input) and another task representation (output). This representation, generated by the mapping network is used to bias the action network, which accomplishes the task itself.

The "homoiconic" part refers to how the model uses the same components (architecture) to operate on the input data (the "task mapping") and to complete the task itself (the "action network").

How it Works

The easiest way to conceive of this model is as a conditional RNN. This is a standard RNN that also accepts a third vector alongside it's usual input. This third vector, the condition, colors or 'conditions' the RNN's output.

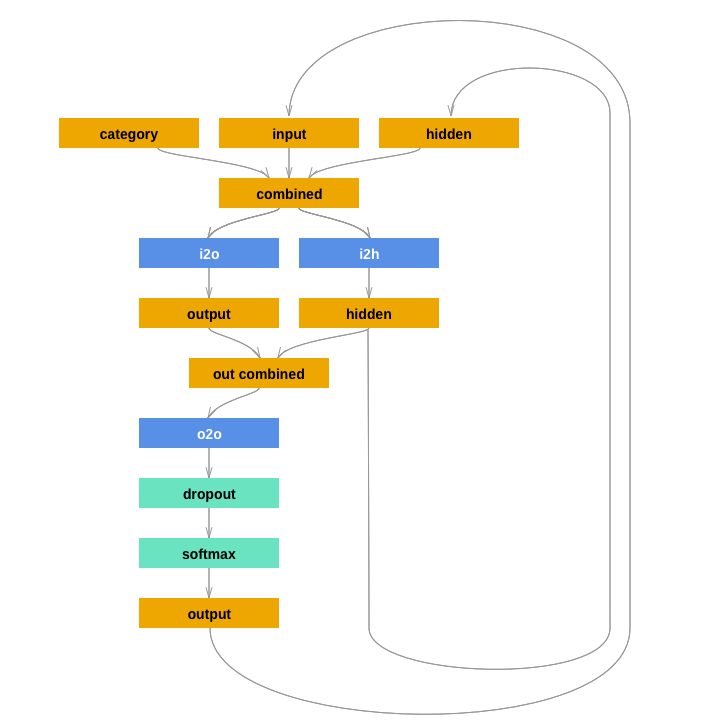
This is the architecture of a conditional RNN, not the meta-mapping network. But notice how the category input (the condition) changes the standard behavior of the RNN. This is a useful analogy for understanding what follows.

Let's go step by step.

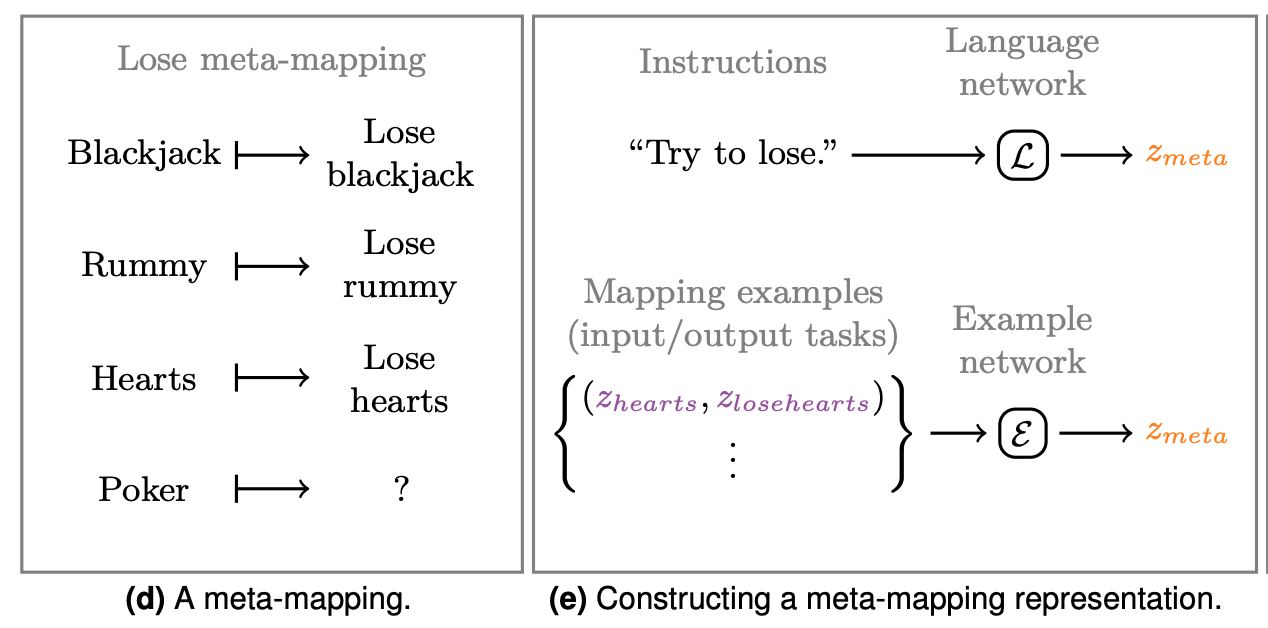
1. Encode the Task With a "Mapping Network"

To achieve meta-mapping, we first must communicate the task to the model.

The paper proposes three ways to encode the task:

1. Written instructions, language model style: "Win at poker"
2. From examples, supervised learning style: "This is what ten thousand winning poker games look like". These are the tuples you'll see in the following image.
3. Transforming a prior task mapping — basically, conditioning on other task mappings. The task mapping "Win at Blackjack" is the starting point for "Win at Poker". More on this later...

We can encode a task via a language model or input/output mappings. This "mapping network" is specific to the task being modeled i.e. convolution for images, LSTM for language etc. This network learns the task mapping.

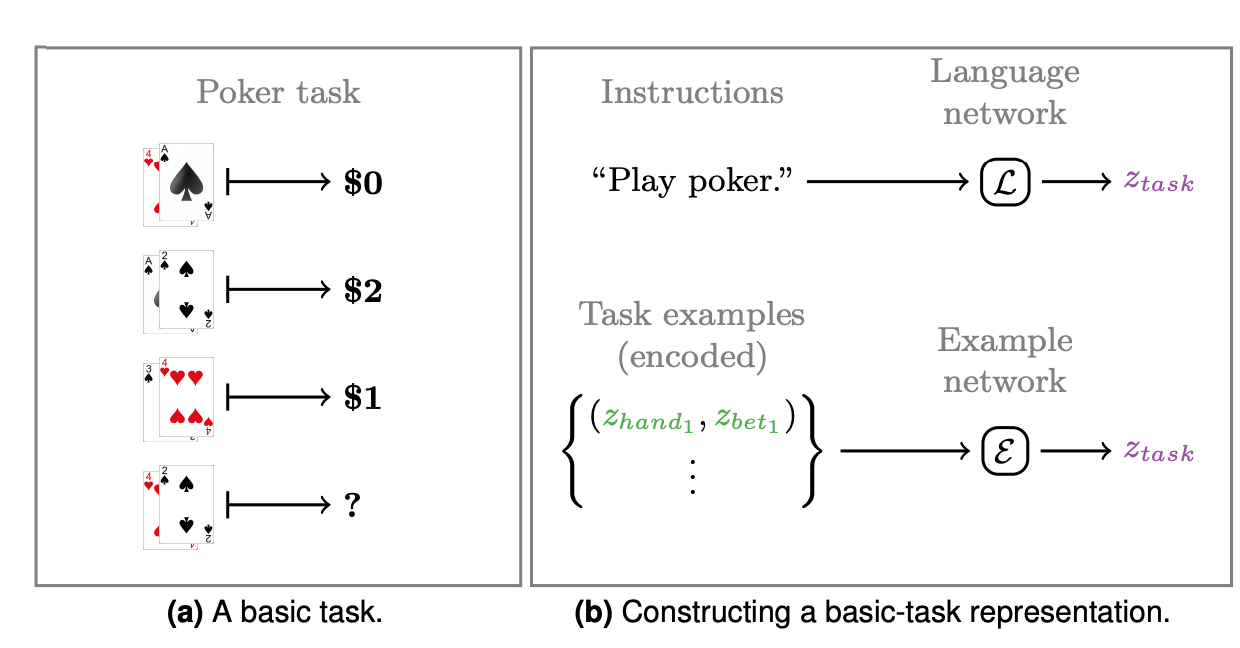
The easiest way to think about this is as an LSTM that you tell "Play poker". The LSTM's output now encodes this task.

2a. Train for the Task

The task mapping is only one input to the model. The rest of the architecture is an end-to-end model for completing the task itself.

We use the encoded task from step 1 as the input to a "HyperNet" (H below). The Hypernet adapts its weights to the encoded task input.

The Hypernet is a sort of encoder for the task representation created by the "mapping network".

The output of the Hypernet is fed into an intermediate network called the "task network". This network is shared between the portion of the architecture concerned with understanding the task mapping and the portion of the network that completes the task itself.

The task network combines the task mapping with the real input for completing the task itself.

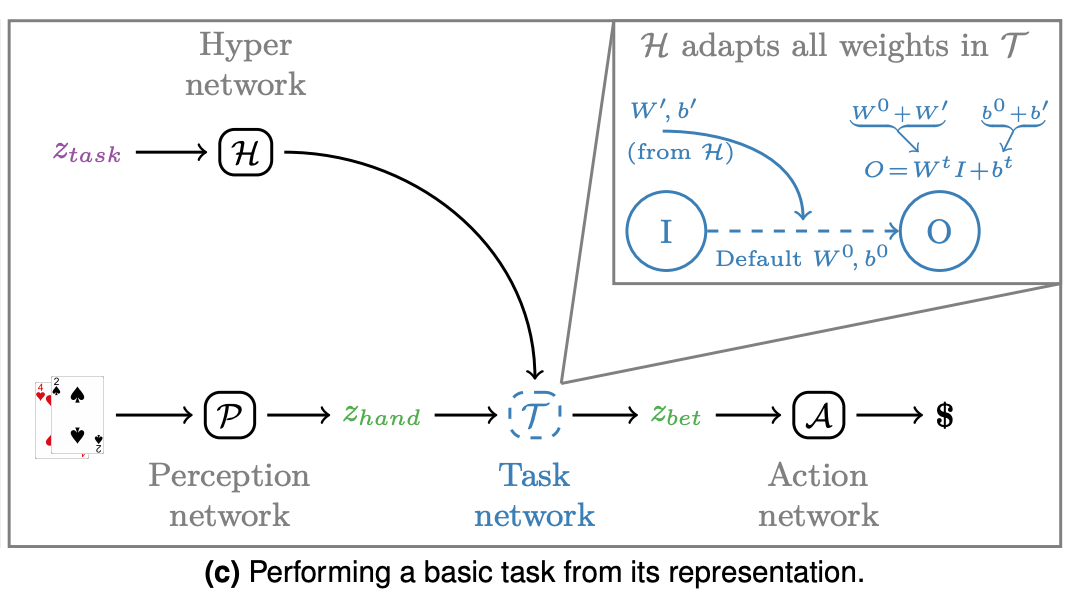
The connections from task mapping to hypernetwork to the task network take us all the way through the portion of the network most concerned with meta-mapping.

The other main piece of the architecture is a sub-network that accomplishes the task itself.

This network "perceives" the input (P) and then receives the Hypernet (H)'s input via the task network. This 'colors' or 'conditions' the perception input with the task mapping e.g. "Win at Poker".

The "Action Network" (A) then decodes the combined perception/task features into an output e.g. a bet in poker.

This gives us an end-to-end system that colors 'perception' with an encoded task and transforms it to a task-relevant output.

2b. Train Meta Mapping

So far we have an end-to-end network that accomplishes a task and colors it with some task mapping input.

Training the mapping step so that it can be used for meta-mapping (the authors' big contribution here) deserves a special note.

To train meta-mapping the author begins with an initial representation of the mapping using examples or language e.g. "Win at poker".

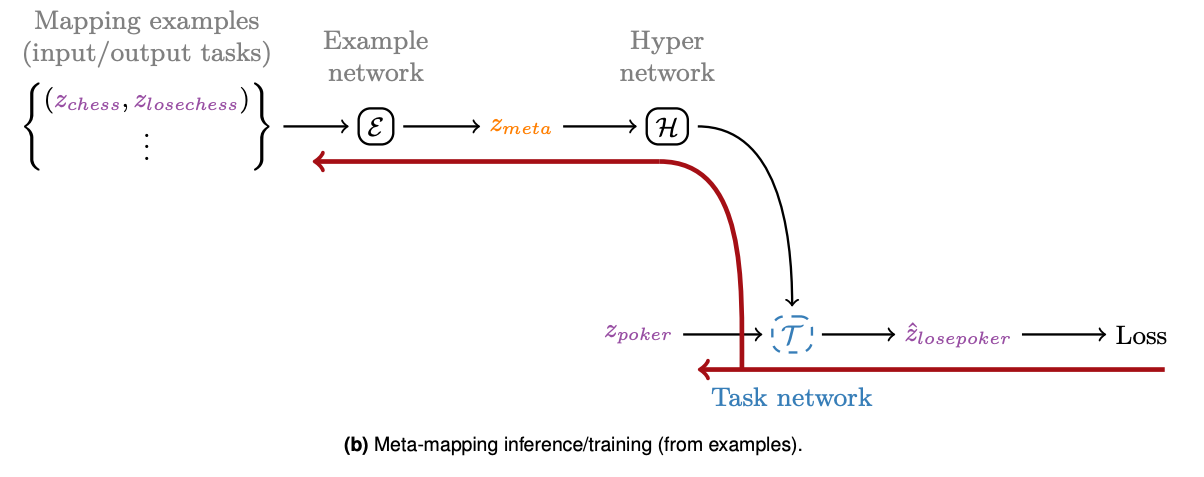
Then task mappings for examples that the model has never seen are fed into the task network. The model minimizes l2 loss between the output embeddings of the "mapping network" (zmeta below) and the embedding output from the task network (zlosepoker below).

In effect, we minimize the loss between the encoded mapping and the encoded task (the output of the task network).

Notice that the task input to the mapping network ("Example Network" below) is different than the input to the task network. In the image, we minimize loss between the task chess/lose chess and poker/lose poker.

In principle, this teaches the the model the concept of "to lose". This "understanding" of the model is useful for meta-mapping task transfer later ("lose at checkers", "lose at blackjack").

3. Adapt the encoded task representation to the new task

We encoded the initial task using a language model or input-output pairs.

To generate a task variation, we feed in different instructions or examples. Instead of "win at poker" we say "lose at poker". Or instead of showing winning poker hands, we show losing poker hands.

Even if the model has never trained to "lose at poker", the task "lose at poker" will reuse weights trained during the meta-mapping training step where it learned how to lose a variety of other games.

With these weights, we can tell the model to lose a new game (zero-shot) and, at least in theory, it should be able to perform the new task.

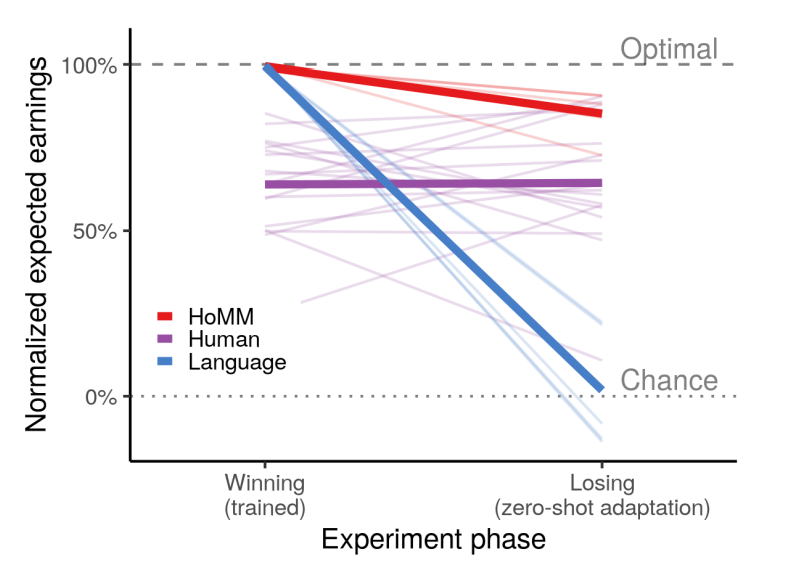
Model Performance

The authors share many experiments which are too many and too varied to get into here. The paper applies meta mapping to card games, polynomial regression, "visual concepts", and Reinforcement Learning.

The results are solid across domains. In poker, for example, the model efficiently switches from winning to losing the game, without ever having trained directly on 'losing'.

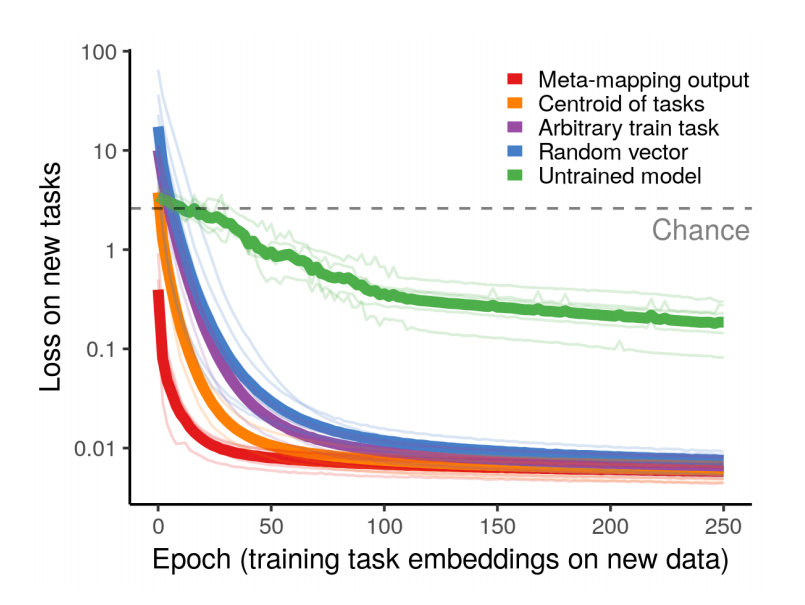
Transfer Learning through Meta Mapping (?)

As for the idea's affects on training time and cumulative error, the authors offer some persuasive graphs.

The author provides a graph that shows significantly faster and better model performance on less data using meta mapping on a regression task.

Citations

Transforming Task Representations To Allow Deep Learning Models to Perform Novel Tasks paper on Arvix

Github Repo for HoMM